Hvad er en eksponentiel funktion?
Den eksponentielle funktion er en af de mest vigtige funktioner inden for matematikken (selvom det må indrømmes, at den lineære funktion rangerer endnu højere i betydning). For at danne en eksponentiel funktion lader vi den uafhængige variabel være eksponenten. Et simpelt eksempel er funktionen:
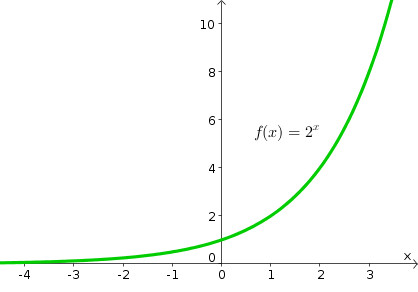
Som illustreret i ovenstående graf for f stiger den eksponentielle funktion hurtigt. Eksponentielle funktioner er løsninger til de enkleste typer af dynamiske systemer. For eksempel opstår en eksponentiel funktion i simple modeller for vækst af bakterier.
En eksponentiel funktion kan beskrive vækst eller forfald.
Eksempel på en Eksponentiel Funktion
At forstå kernen i eksponentielle funktioner er afgørende for enhver, der ønsker at navigere gennem kompleks matematik. En eksponentiel funktion repræsenteres matematisk som f(x)=a⋅bx, hvor er en konstant og er en positiv konstant forskellig fra 1.
Anvendelser i Virkeligheden
Eksponentielle funktioner er ikke kun teoretiske koncepter; de findes i vores daglige liv. Fra økonomi til videnskab styrer disse funktioner vækst og fald. For eksempel styrer de økonomiske markeder, hvordan priser stiger eller falder over tid.
Implementering i Teknologi
Teknologiens verden er også dybt forankret i eksponentielle funktioner. Fra computeres ydeevne til datalagringskapacitet er disse funktioner afgørende for teknologiske fremskridt.
Find x og y i eksponentiel funktion
At finde værdierne af x og y i en eksponentiel funktion kan nogle gange virke udfordrende, men ved at følge bestemte skridt, kan disse værdier blive beregnet præcist. Det første skridt er at få isolaret x, hvilket indebærer at ændre ligningens struktur, så x står alene. Dette kan kræve anvendelse af logaritmer eller andre matematiske principper for at manipulere ligningen korrekt. Efter x er isoleret, kan ligningen omstruktureres for at finde y’s værdi ved at erstatte x med den beregnede værdi.
Hvis du støder på problemer undervejs, eller hvis du ønsker at validere dit resultat, kan det være en god ide at skrive det i webmatematiks forum. Her kan erfarne matematikere og andre studerende tilbyde vejledning og feedback. Derudover kan webmatematiks videobibliotek indeholde en relevant videolektion, der trin for trin gennemgår processen med at finde x og y i en eksponentiel funktion, hvilket kan være yderst hjælpsomt for visuelle lærere.
Bestem forskrift for eksponentiel funktion ud fra to punkter
I matematik C på htx lærer man om eksponentielle funktioner og hvordan man finder deres forskrift, især når man har givet to punkter. Denne metode kræver forståelse for beregning af både basen og potens i funktionen. For at isolere x, og dermed finde en x-værdi som er større end nul, er det ofte nødvendigt at anvende en logaritmisk tilgang. Når x-værdien vokser med en fast rate, det vil sige, så vokser funktionsværdien også på en bestemt måde, som ofte kan beskrives som en ret linje på et logaritmisk papir.
Forståelse af relative tilvækst er afgørende, fordi det hjælper med at bestemme forskriften ud fra de givne punkterne. Dette koncept er særligt relevant, når man arbejder med fænomener, hvor noget henfalder over tid, såsom et radioaktivt stof der henfalder med hvert x (år der går). Hvis du ønsker at forstå denne proces bedre, kan du læse mere på webmatematiks forum, hvor der ofte er hjælp at hente eller spørgsmål at stille. Her kan man også finde videolektioner, som trin for trin viser beregningen, og hvordan du kan have fået samme resultat. Husk, at præcision i beregningen sikrer, at når du tegner funktionen, afspejler den den relative tilvækst korrekt.
Eksponentielt voksende eller eksponentielt aftagende
I matematik støder vi ofte på begreberne eksponentielt voksende eller eksponentielt aftagende. Dette handler grundlæggende om funktioner, der kan beskrives ved en ligning, hvor x og y er variable, og værdierne af y vokser eller aftager i takt med at x-værdien vokser. Typisk ser vi på en funktion på formen y = ab^x, hvor a repræsenterer skæringen med y-aksen, og b er fremskrivningsfaktoren, der fortæller om funktionen vokser eller aftager. Når vi skal beregne b eller a, handler det om at isolere disse, for at forstå hvordan y vokser i forhold til x. Dette gør, at vi kan forudsige beløb på f.eks. en bankkonto over et antal år, hvis vi kender fremskrivningsfaktoren.
I forbindelse med at finde værdierne for a og b i en funktionsforskrift, er det vigtigt at forstå konceptet med relativ tilvækst, som er centralt i eksponentiel vækst eller aftagelse. For at beregne b, kan det være nødvendigt at isolere b, hvilket ofte indebærer en omformulering af funktionsforskriften således at b allerede er isoleret. Herefter kan man indsætte kendte værdier for at beregne den specifikke værdi af b. Dette trin er afgørende for at kunne forstå, hvordan y vokser eksponentielt i forhold til x. Interaktionen mellem x og y, hvoraf væksten eller aftagelsen er afhænger
Eksempel på eksponentiel vækst
En eksponentiel funktion er en funktion, der kan beskrives ved forskriften for den eksponentielle funktion. Forskriften angiver hvordan y-værdien af funktionen beregnes ud fra den isolerede x-værdien. I matematik skrives en eksponentiel funktion ofte på formen f(x) = c * b^x, hvor c er begyndelsesværdien og b er en fremskrivningsfaktoren. Eksempel på eksponentiel vækst kan være en saldoen på en opsparingskonto, hvor rente tilskrives årligt. Grafen for en eksponentiel udvikling vil have en skæring med y-aksen i begyndelsesværdien og en stigning, der er større end 1.
Ved at beregne konstanten b, kan vi bestemme hvor hurtigt y-værdien vokser, og dermed beskrive den eksponentielle udvikling mere præcist. Forskellen mellem en eksponentiel funktion og en lineær funktion er, at i en eksponentiel funktion aftager x-værdieny-værdien vokser. På webmatematik kan du finde noter til eksponentielle funktioner, der forklarer formlen for den eksponentielle funktion mere detaljeret, samt hvordan eksponentielle udviklinger kan beskrives ved hjælp af fast procent y.