Pythagoras læresætning, som også bare kaldes for Pythagoras’ sætning, forklarer forholdet mellem de tre sider af en retvinklet trekant. Læresætningen er denne:
Kvadratet på hypotenusen i en retvinklet trekant er lig summen af kateternes kvadrater.
En retvinklet trekant er en trekant hvor en af vinklerne i trekanten er 90 grader. Her er et eksempel på en retvinklet trekant:
Indholdsfortegnelse
ToggleForklaring af Pythagoras’ læresætning
Pythagoras-sætningen siger, at hvis en trekant er retvinklet, så er kvadratet på hypotenusen lig med summen af kvadraterne på de to andre sider. For at forklare dette nærmere, er der her et eksempel på dette:
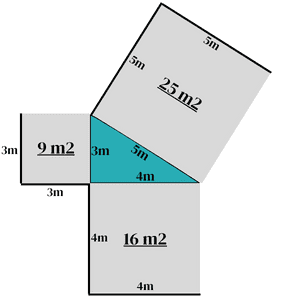
Hvis der laves et kvadrat ud fra hver linje i den retvinklede trekant, er arealet at hypotenusens (den længste linje) kvadrat, lige så stort som arealet af de 2 resterende kvadrater til sammen.
Som det kan ses i eksemplet ovenover, er arealet af hypotenusens kvadrat 25 m², samtidig med at arealet af ”kateternes” kvadrater er henholdsvis 9 m² og 16 m². Dette bringer os videre til ligningen/formlen for Pythagoras’ læresætning.
Pythagoras formel
Formlen for Pythagoras’ læresætning er:
c² = a² + b²
c = hypotenusen af den retvinklede trekant.
a = det ene kateter
b = det andet kateter
Hvis vi overfører dette til vores eksempel fra før, så ser formel således ud:
5² = 4² + 3²
Udregnet:
25 = 16 + 9
25 = 25
Dermed går det hele op!
Formålet med Pythagoras’ formel
Men hvad er formålet med Pythagoras’ formel?
Formålet er, at du altid kan finde længden af alle sider af en trekant, hvis du bare kender målene på 2 af siderne.
Dermed kan dette bruges til opgaver, hvor en af siderne i en retvinklet trekant er ukendt. Se f.eks. i vores eksempel, hvis vi gør 1 af siderne ukendte:
x = 4² + 3²
Udregnet:
x = 16 + 9
Dermed kan vi lægge 16 og 9 sammen, for at finde x:
X = 25
Hvis vi så ønsker at finde længden af hypotenusen, mangler vi en ting. Dette er nemlig at finde kvadratroden, da de 25 var ganget op med ”i anden”. Kvadratroden af 25 er 5, og dermed har vi fundet længden af hypotenusen.
